Imagine you are the Head of Operations at the contact center for New York City's largest municipal information service, 311. You've just learned (as did the author of this post) that 311 is not just a call center, but in fact receives inquiries via their website. You're the Head of Operations, so you're extremely embarrassed that you didn't know this. You need to act quickly (and discreetly) to resolve all of these electronic inquiries before Bill de Blasio lays the hammer down on you.

You recognize that 311 requests are often highly locale-specific, and the best way to ensure that your staff can knowledgeably field requests is to have them specialize in a particular geographical area. But your staff, who now severely question your competence, will stage a mutiny if there is any perceived unfairness in the way that you assign the work to the agents. So you need to make sure that you evenly distribute the queue of unresolved requests amongst them.

What you have on your hands is an optimization problem. You are trying to ensure that workload gets balanced amongst agents, and that agents each field requests from a specific geography. These two goals can be at odds with each other, and you could never manually go through all of the possibile assignment permutations to find the right solution. Luckily, you have a brilliant Data Scientist (who is also the author of this post) to help get you out of this pickle.

To figure out how to solve this problem, we first need to understand the data that we have at our disposal. Below is an example of the data we have available for one unresolved request:

The column names are a bit cut off, but we can immediately see that the only bit of geographical information we have associated with the request is the zip code that the request came from (in this case 10011). Because of this, we know we will have to assign requests to agents based on Zip Code if we want agents to be geographically-specialized.

We've established that we will assign zip codes (and all of the requests from that zip code) to agents. But before we can do that, we need to choose a data structure to work with that can encapsulate the following:

1. How close a zip code is to another one (so that we can try to assign proximal zip codes to the same agent)
2. How many requests are coming from a zip code (so that we can assign zip codes to agents in such a way that keeps workload balanced)

One data structure that can accomplish such a feat is a Weighted Graph. A graph is comprised of vertices (aka nodes) and edges that connect one vertex to another. In a weighted graph, vertices and edges can have numerical values. To help illustrate how a Weighted Graph can be applied to our problem, the image below shows what a graph would look like if it included just three zip codes:

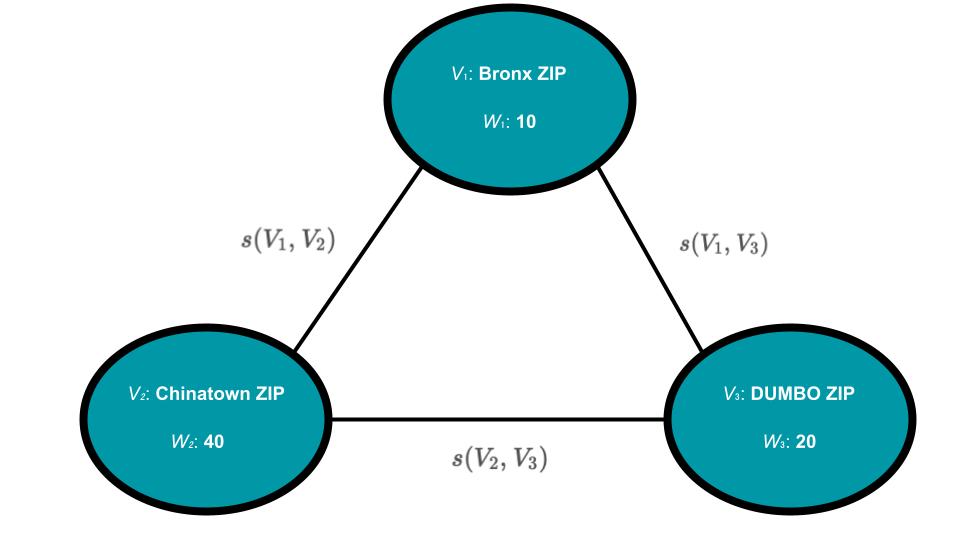
Where:

• $V$₁ = Vertex 1. Corresponds to a particular zip code (in our example, a zip code in the Bronx)
• $W$₁ = The Weight of Vertex 1. Corresponds to the number of unresolved requests coming from that zip code
• $S(V$₁, V₂) = The weight of the edge, or Similiarity, between Vertex 1 and Vertex 2. Because we need to represent geographic proximity, we can use the inverse distance between two zip codes as the edge weight between them.

Now imagine this Graph with all of the zip codes in New York City, and you have our data structure for this problem.

Now that we've defined our business problem and learned about Graphs, we are ready to formalize our optimization problem. First, though, let's break down the business requirements and translate them into technical terms that will help us define our optimization problem:

Business Objective	Technical Translation
1. Divvy up all the NYC zip codes amongst available agents	1. Partition the Graph into k Sub-Graphs***
2. Agents should be assigned zip codes that are close to each other	2. The partition should minimize the sum of the weights of edges that get removed by the partition***
3. Agents should be assigned the same amount of work	3. The sum of the vertex weights should be relatively balanced (as defined by some balance threshold) across all Sub-Graphs created by the partition***

***In case I've lost you with some of the technical terms I've just introduced here, let's go back to our toy example. Imagine you took a pair of scissors and cut the lines that connected the Chinatown Vertex to the other Vertices in the graph. You have partitioned the graph into two distinct sub-graphs. The lines that you cut to partition the graph are the edges that got removed by the partition.

Optimization problems are math problems, so we need to use our technical requirements to define an Objective Function (a value that we seek to either minimize or maximize) and constraints (conditions that, if not met, constitute a "failure" to solve the problem).

Objective Function

Our objective function, which we will call our "Minimum Cut Objective", is already laid out for us in Technical Requirement #2 in the table above: We want to minimize the sum of the edge weights that get removed/"cut" by the partition. Our Min. Cut Objective stated mathematically is:

`min_(Deltaepsilon) sum_((a,b)inDeltaepsilon) s(V_a, V_b)`

Where:

• `Deltaepsilon` is the set of edges that get removed as a result of the partition.
• `s(V_a, V_b)` is the weight of the edge connecting vertices `V_a` and `V_b`

Constraints

Now we need to add a constraint to our problem so that we can account for Technical Requirement #3: Ensuring that all sub-graphs are balanced w/r/t to total vertex weight. To state this "Balance" constraint mathematically:

`max_(lin{1,...,k}) sum_(lambda_j = l) w_j <= t cdot frac{sum_(i=1)^n w_i}{k}`

Where:

• `max_(lin{1,...,k}) sum_(lambda_j = l) w_j` is the summed-vertex-weight of the largest sub-graph created by the partition
• `sum_(i=1)^n w_i` is the sum of all vertex-weights in entire graph
• `k` is the number of sub-graphs created by the partition.
• `t` is a balance-threshold that we can tune based on how balanced we want the sub-graphs to be.

Putting this constraint all together, we are saying that the largest sub-graph created by the partition (in terms of summed-vertex-weight) must be less than or equal the average summed-vertex-weight of the sub-graphs times some balance threshold, `t`. If we set `t=1`, we're saying that all sub-graphs must be exactly balanced.

In setting up our Optimization Problem, we have defined what exactly constitutes a "solution" -- but we still need to find that solution. To do so, and to do so efficiently, we have to enlist an algorithm.

There is a brute force algorithm that can be described in pretty straight-forward terms: Go through every possible permutation of assigning zip codes to agents. The "best" assignment will be the one is associated with the lowest value for Min. Cut. Objective Function that does not violate the Balance Constraint.

While this brute-force algorithm will find the optimal solution in theory, in practice it is not feasible. Why not? Because even a computer would spend the rest of eternity going through every possible permutation of assignments, so our algorithm would never finish. We need to find an algorithm that can efficiently find a solution to our problem, so for that we turn to an open-source algorithm called the METIS algorithm.

The METIS Algorithm

In our toy example of three Zip Codes (pictured above), there are only three possible ways to divvy up the zip codes amongst two Agents (assuming it matters which agents get which zip codes). If we try to divide 90 zip codes amongst two agents, there are over 618 septillion (a word that the author of this post learned today) possibilities. So can we somehow find a way to intelligently reduce the number of vertices (zip codes) in our graph to reduce the number of combinations and therefore make the problem feasible? This is what the METIS algorithm attempts to do.

METIS has three "phases" to it, which can be described generally as:

1. The Coarsening Phase: In this phase, similar vertices (similarity as determined by the edge weights between them) are collapsed together to form super-vertices. The vertex-weight and edge-weights of these super-vertices are summed up from the original vertices that comprise them, thereby preserving pertinent information from the original graph. This collapsing process happens repeatedly, and at the end of this phase, you will have a "coarsened" graph: A graph with many fewer vertices than the original one.
2. The Initial Partitioning Phase: In this phase, the coarsened graph from the first phase is partitioned in accordance with our optimization problem: the egdes connecting the super-vertices are cut in such a way to minimize the edge-weights that are getting cut, and in a way that keeps the resulting sub-graphs balanced.
3. The De-coarsening / Refining Phase: In this phase, we reverse the steps taken during the coarsening phase: super-vertices get split into their composite vertices. Each time we do this, we are re-introducing more vertices into the graph, so the partition that was found during the Initial Partitioning phase may no longer be optimal because we are introducing more degress of freedom. So this parition gets "refined" as we move along to our original graph.

This description of the phases is a very high-level overview. If you are curious to learn more, you can read the (painfully detailed) paper titled A fast and high quality multilevel scheme for partitioning irregular graphs by George Karypsis and Vipin Kumar, who also developed the open-source software that was adopted for this project.

But if you are looking for an even more general description, you can use the analogy of a lazy but crafty manager who says: "I don't want to go through the work of assigning all these zip codes to my agents, so instead I'll first assign them boroughs, and if things feel uneven I'll start swapping out neighborhoods between them, and then at the end I'll start swapping zip codes at the boundaries of neighborhoods until things are fair."

In the linked demo, you can input how many agents you have available to work through the open requests and find the best way to divvy up the work. An example of the results if you have 5 agents:

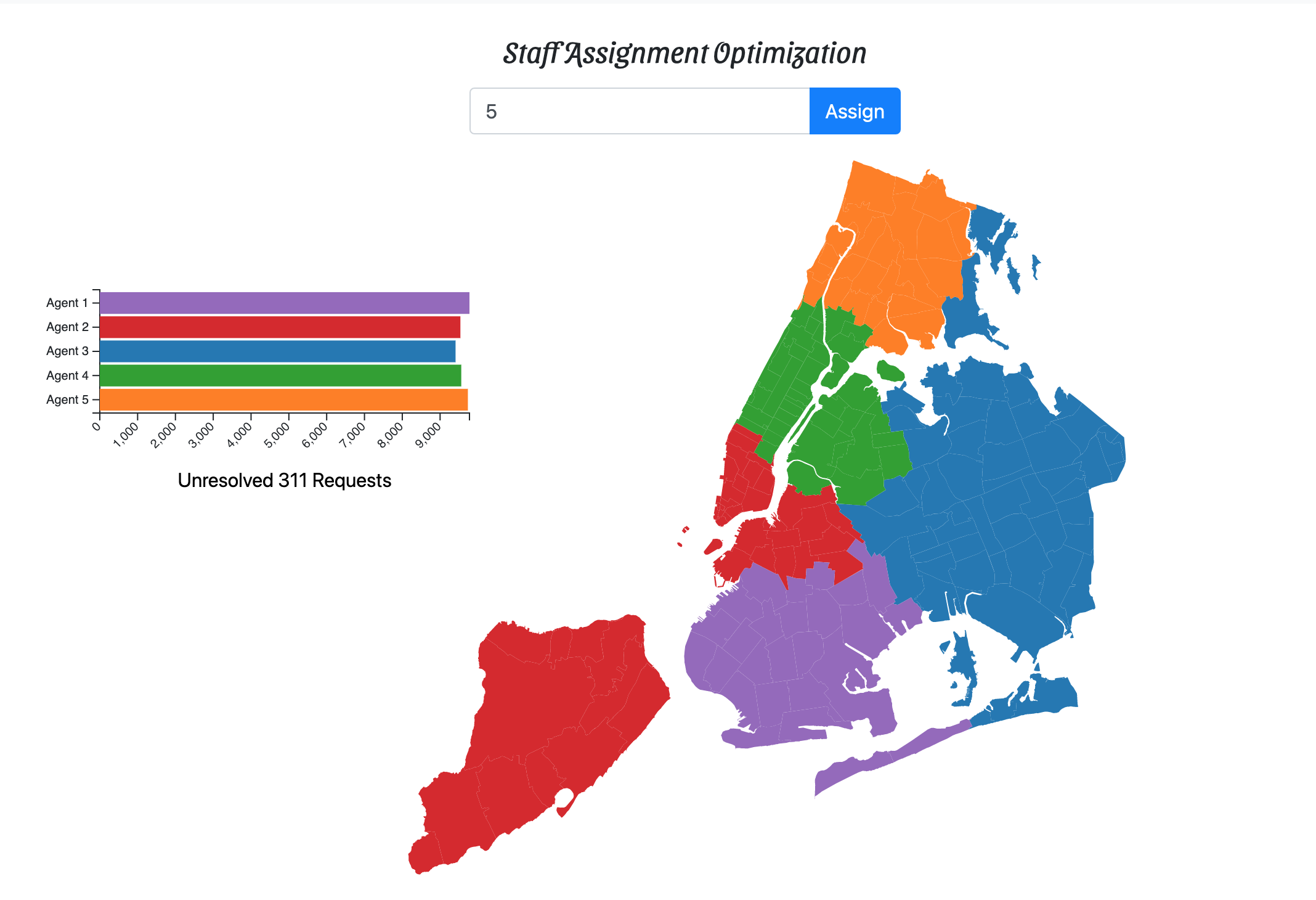
Now get to work! You and your team have some angry New Yorkers to appease.